

- #Calculate standard error of the mean how to#
- #Calculate standard error of the mean install#
- #Calculate standard error of the mean code#
We seen that for data1 the SEM is 1.149 and for data2 SEM is 11.177. The Standard error of the mean for the repeated dataset : 11.177
#Calculate standard error of the mean code#
The Output of the above code is shown below:- #Output data1 & data2 where data2 is created by replacing the last value with 120. In the above example, we created the two datasets i.e. #define dataset 2 by replace last value with 120 Let’s discuss this with below example:- #import modules Values of data2 are less spread out around the mean as compared to data1, although both have the same mean value.Ģ The Value of SEM : The larger value of the SEM indicates that the values are more spread around the mean. It clearly shows that with an increase in size the SEM decreases. We seen that for data1 the SEM is 1.149 and for data2 SEM is 0.791. The Standard error of the mean for the repeated dataset : 0.791 The Standard error of the mean for the original dataset: 1.149 The Output of the above code is shown below:- # Output data1 & data2 where data2 is just the twice of data1. Print("The Standard error of the mean for the repeated dataset : %.3f"%result2) Print("The Standard error of the mean for the original dataset: %.3f"%result1) #define dataset 2 by repeated the first dataset twiceĭata2 = Let’s see this with below example:- #import modules The two important factors to keep in mind while interpreting the SEM are as follows:-ġ Sample Size:- With the increase in sample size, the standard error of mean tends to decrease.
#Calculate standard error of the mean how to#
The Standard error of the mean : 1.149 How to Interpret the Standard Error of the Mean Using sem() function we calculated the standard error of the mean. Lets calculate the standard error of mean by using below python code.
#Calculate standard error of the mean install#
pip install scipy Example 2: How to calculate SEM in Python If you don’t have the scipy library installed then use the below command on windows command prompt for scipy library installation. We will be using Scipy library available in python, it provides sem() function to calculate the standard error of the mean. The Output of the above code is shown below. Note that we must specify ddof=1 in the argument for std() function to calculate the sample standard deviation instead of population standard deviation. Using std() function we calculated the standard error of the mean. In the above code, we import numpy library to define the dataset. Print("The Standard error of the mean : %.3f"%result) Result = np.std(data, ddof=1) / np.sqrt(np.size(data)) Let’s understand, how to calculate the standard error of mean (SEM) with the given below python code. pip install numpy Example 1: How to calculate SEM in Python
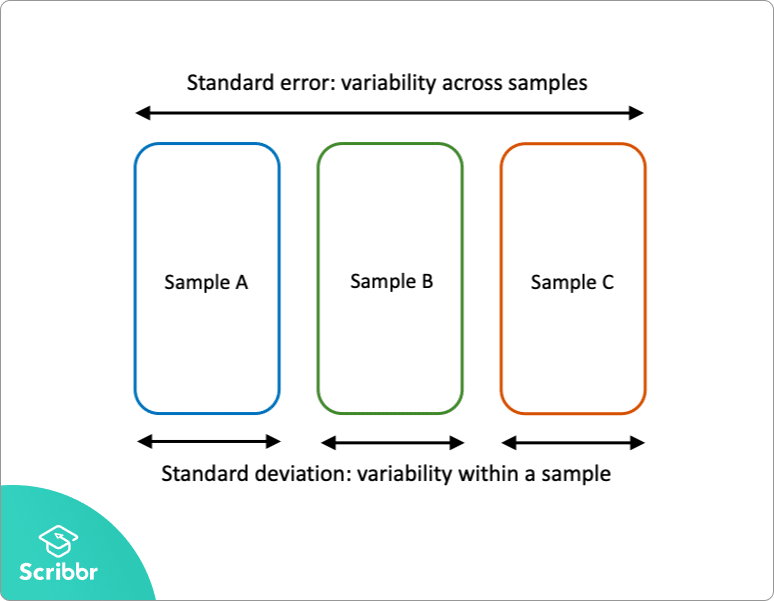
If you don’t have numpy package installed, use the below command on windows command prompt for numpy library installation. We will be using the numpy available in python, it provides std() function to calculate the standard error of the mean. Standard error of the mean (SEM) = s / √n The Standard error of the mean for a sample is calculated using below formula: 7 Conclusion Standard Error of the Mean Formula


 0 kommentar(er)
0 kommentar(er)
